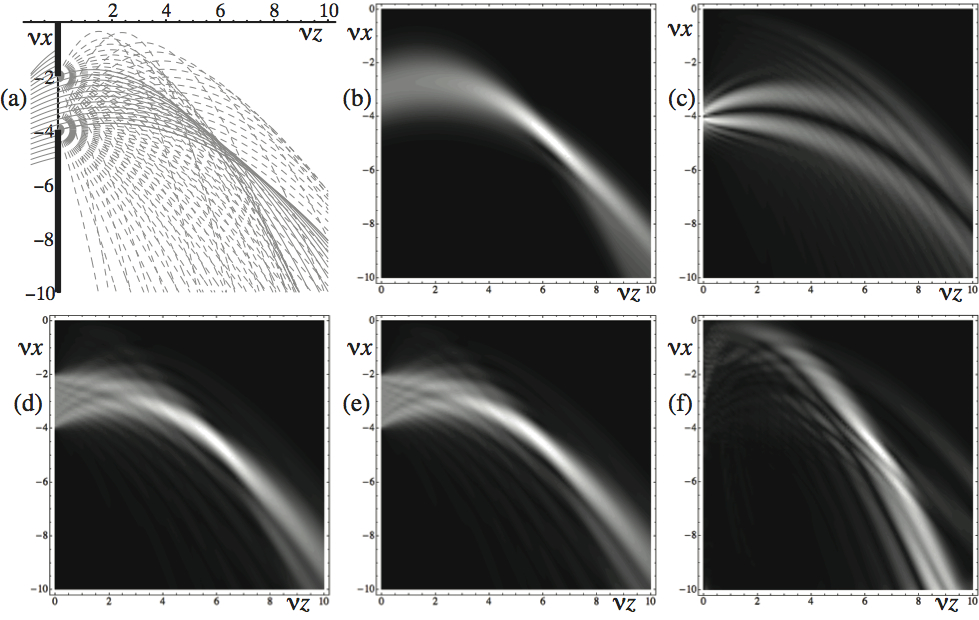
We study the propagation of coherent wave fields through homogeneous or inhomogeneous media in terms of rays through a method called stable aggregates of flexible elements (SAFE). The wave field is constructed by “dressing” the rays with field contributions of Gaussian profile. While each of these contributions is not an approximate solution to the wave equation, their superposition is. This superposition is asymptotically independent of the width of the contributions assigned to the rays.
Within the context of quantum-mechanical applications, this method can be used to model the evolution of wavefunctions in different potentials, and can be regarded as an initial value representation.
Book chapter giving an overview of ray-based methods for wave propagation
Stable aggregates of flexible elements in optics and quantum mechanics
Journal articles
- M.A. Alonso, “Ray-based diffraction calculations using stable aggregates of flexible elements,” J. Opt. Soc. Am. A 30, 1223-1235 (2013).
- M.A. Alonso and G.W. Forbes, “Stable aggregates of flexible elements give a stronger link between rays and waves,” Opt. Exp. 10, 728-739 (2002).
- M.A. Alonso and G.W. Forbes, “Using rays better. III. Error estimates and illustrative applications in smooth media,” J. Opt. Soc. Am. A 18, 1357-1370 (2001).
- M.A. Alonso and G.W. Forbes, “Using rays better. II. Ray families to match prescribed wave fields,” J. Opt. Soc. Am. A 18, 1146-1159 (2001).
- G.W. Forbes and M.A. Alonso, “Using rays better. I. Theory for smoothly varying media,” J. Opt. Soc. Am. A 18, 1132-1145 (2001).
- M.A. Alonso and G.W. Forbes, “New approach to semiclassical analysis in mechanics,” J. Math. Phys. 40, 1699-1718 (1999).
Conference proceedings
- M.A. Alonso, “The connection between rays and waves,” Proceedings of Fringe 2013, 7th International Workshop on Advanced Optical Imaging and Metrology, W. Osten, Ed. (Springer, Hiedelberg, 2013), pp. 457-466.
- G.W. Forbes and M.A. Alonso, “Stable aggregates of flexible elements link rays and waves,” Nonimaging Optics: Maximum Efficiency Light Transfer VII, SPIE Proceedings 5185, 125-136 (2004).
- M.A. Alonso, “Stable aggregates of flexible elements: Making a silk purse from sow’s ears,” 2004 URSI EMTS International Symposium on Electromagnetic Theory Proceedings (Edizioni Plus, Pisa 2004), pp. 346-348.
- G.W. Forbes and M.A. Alonso, “The Holy Grail of ray-based optical modeling,” Proceedings of the International Optical Design Conference 2002, SPIE Proceedings 4832, 186-197 (2002).
- G.W. Forbes and M.A. Alonso, “What on earth is a ray and how can we use them best?,” Proceedings of the International Optical Design Conference 1998, SPIE Proceedings 3482, 22-31 (1999).
Others
- M.A. Alonso, “La théorie ondulatoire de Fresnel a-t-elle tué les rayons ? Comment réconcilier les rayons et les ondes,” Photoniques, 2020, p. 29-33.
- G.W. Forbes and M.A. Alonso, “Using rays better,” summary included in the Optics in 2001 special issue of Optics and Photonic News 12, 54 (December 2001).
Precursors to SAFE: ray-based propagators and fractional Fourier and Legendre transformations
Journal articles
- G.W. Forbes and M.A. Alonso, “Asymptotic estimation of the optical wave propagator II: relative validity,” J. Opt. Soc. Am. A 15, 1341-1354 (1998).
- M.A. Alonso and G.W. Forbes, “Asymptotic estimation of the optical wave propagator I: derivation of a new method,” J. Opt. Soc. Am. A 15, 1329-1340 (1998).
- M.A. Alonso and G.W. Forbes, “Uniform asymptotic expansions for wave propagators via fractional transformations,” J. Opt. Soc. Am. A 14, 1279-1292 (1997).
- M.A. Alonso and G.W. Forbes, “Semigeometrical estimation of Green’s functions and wave propagators in optics,” J. Opt. Soc. Am. A 14, 1076-1086 (1997).
- M.A. Alonso and G.W. Forbes, “Generalization of Hamilton’s formalism for geometrical optics,” J. Opt. Soc. Am. A 12 2744-2752 (1995).
- M.A. Alonso and G.W. Forbes, “Fractional Legendre transformation,” J. Phys. A: Math. Gen. 28, 5509-5527 (1995).
Conference proceedings