Structured light: ray, wave and polarization aspects
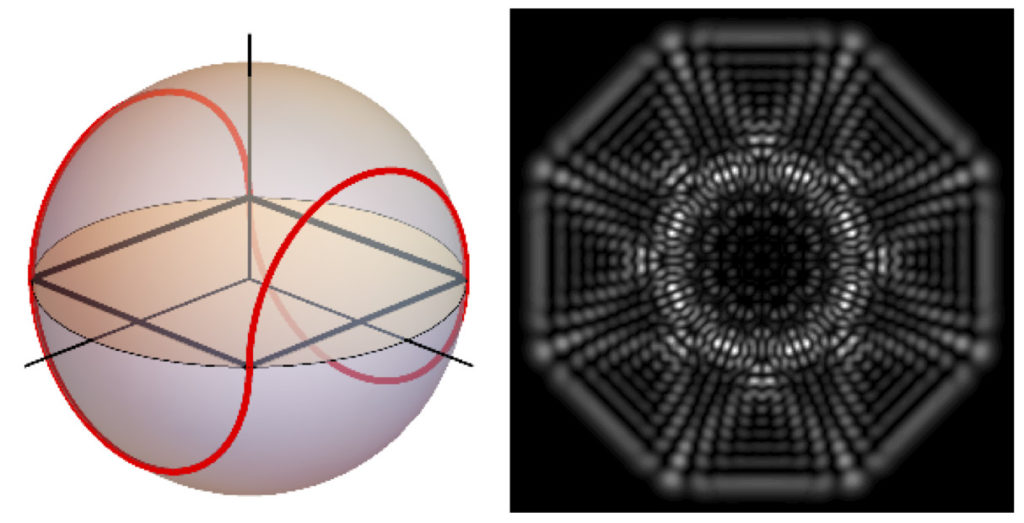
Optical beams and fields that preserve their intensity profile under propagation, full Poincaré beams which cover all possible polarizations, and aspects of orbital and spin angular momentum of light.
See publications on this topic.
Spatially-varying birefringence and geometric phase
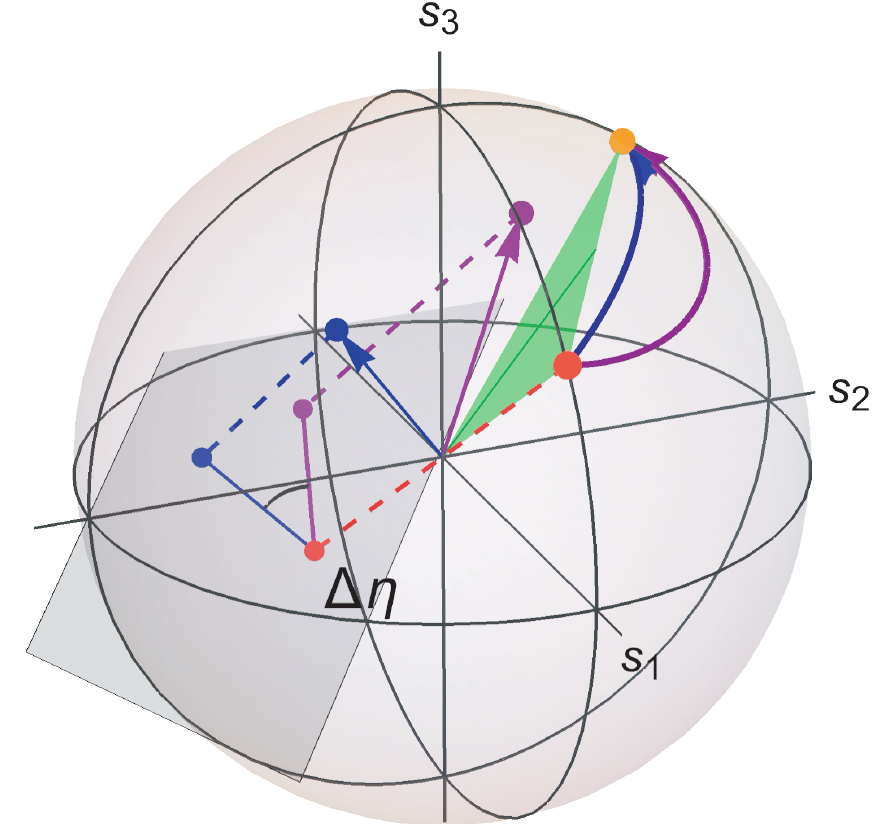
Geometric phases in optics and their application through optical elements with spatially-varying birefringence.
See publications on this topic.
Metrology and measurements

Measurements of polarization, spatial coherence, and applications in microscopy. Measurements of nanostructures using structured focused illumination.
See publications on this topic.
Propagating wave fields using rays
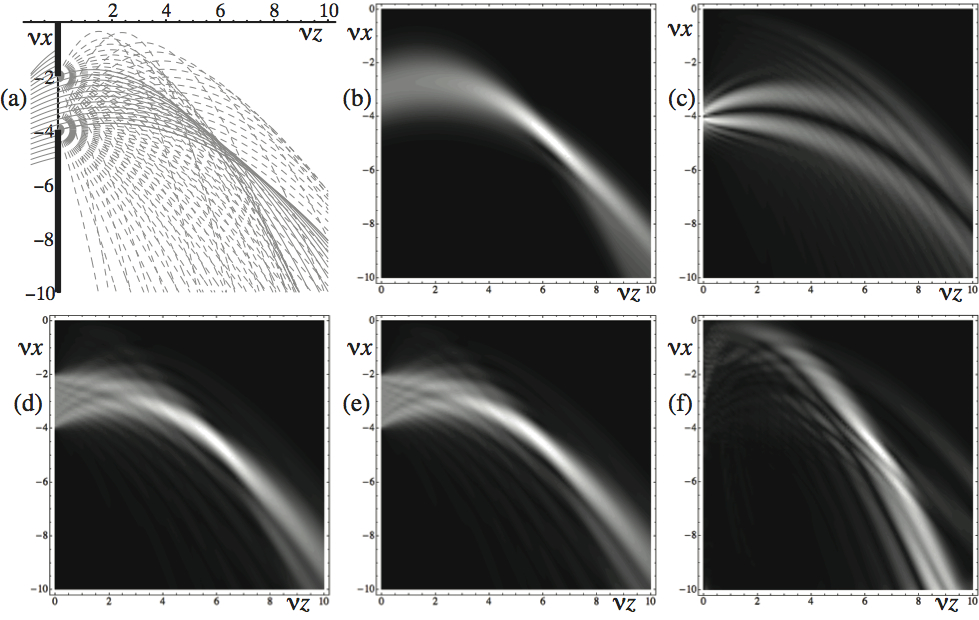
We study the propagation of coherent wave fields through homogeneous or inhomogeneous media in terms of rays through a method called stable aggregates of flexible elements (SAFE). The wave field is constructed by “dressing” the rays with field contributions of Gaussian profile. While each of these contributions is not an approximate solution to the wave equation, their superposition is. This superposition is asymptotically independent of the width of the contributions assigned to the rays.
Within the context of quantum-mechanical applications, this method can be used to model the evolution of wavefunctions in different potentials, and can be regarded as an initial value representation.
See publications on this topic.
Nonparaxial fields: spin-orbit interaction, basis expansions, and interaction with particles
This work consists of analytic models for describing monochromatic fields focused beyond the paraxial regime, including aspects such as fundamental relations related to focal properties, the effects of polarization, closed-form complete orthonormal basis expansions (nonparaxial generalizations of Laguerre-Gaussian beams), and generalizations of Mie theory describing the interaction of these fields with spherical scatterers.
See publications on this topic.
Uncertainty relations and their applications in optics
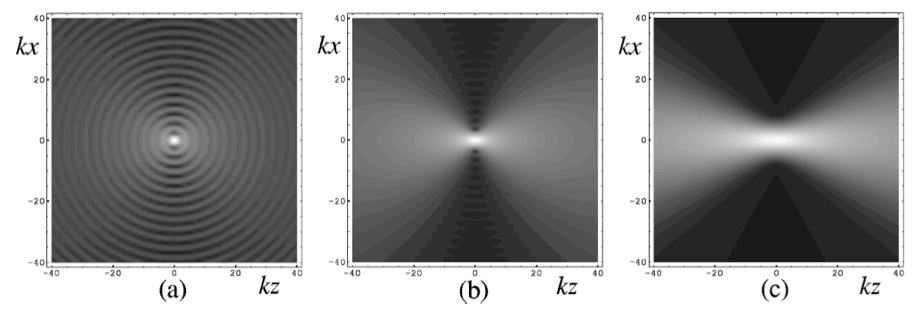
This work includes the definition of measures of spread for periodic distributions (e.g., over a circle or a sphere), the uncertainty relations these measures satisfy, and applications to nonparaxial fields and short pulses.
See publications on this topic.
Wigner functions for describing wave fields and pulses
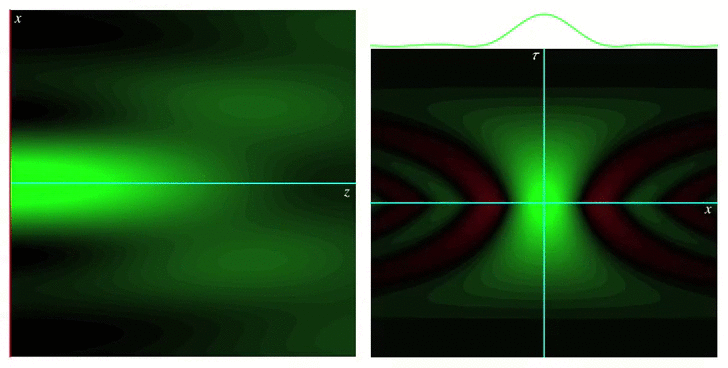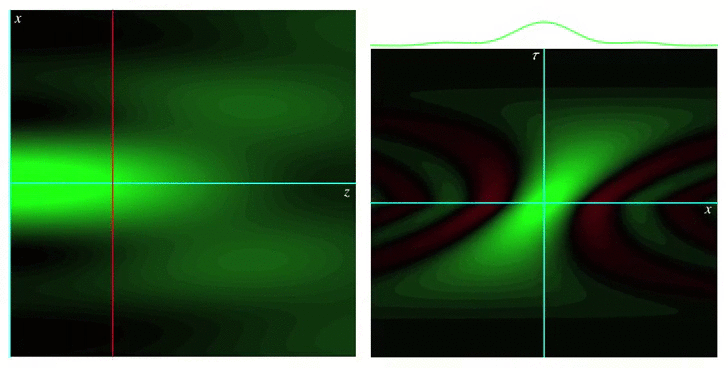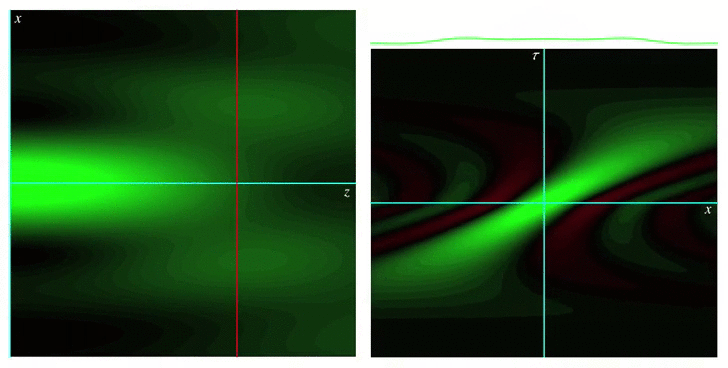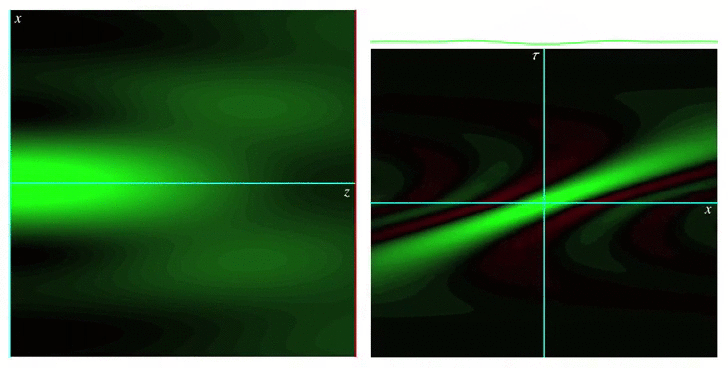
The Wigner function or Wigner distribution is a bilinear integral transformation that allows representing a function jointly in terms of its original variable and its Fourier conjugate. For example, by using the Wigner function, a time signal representing a piece of music can be represented jointly in terms of time and frequency, providing a representation qualitatively similar to a musical score. Wigner functions were first defined by Eugene Wigner in 1932 to describe the wavefunction of a quantum particle in terms of both position and momentum, hence providing a classical-like picture. They also have been applied to modeling the propagation of optical wave fields in terms of rays, and also for the propagation of optical pulses through simple dispersive media.
Our group’s work on Wigner functions and other phase space representations has included studying their behavior in certain limits, as well as providing new definitions for them that are best suited for describing different physical situations, such as nonparaxial propagation of scalar and electromagnetic fields, diffraction effects, propagation of pulses through transparent media with arbitrary dispersion properties, and wave fields constrained to simple curved spaces.
See publications on this topic.
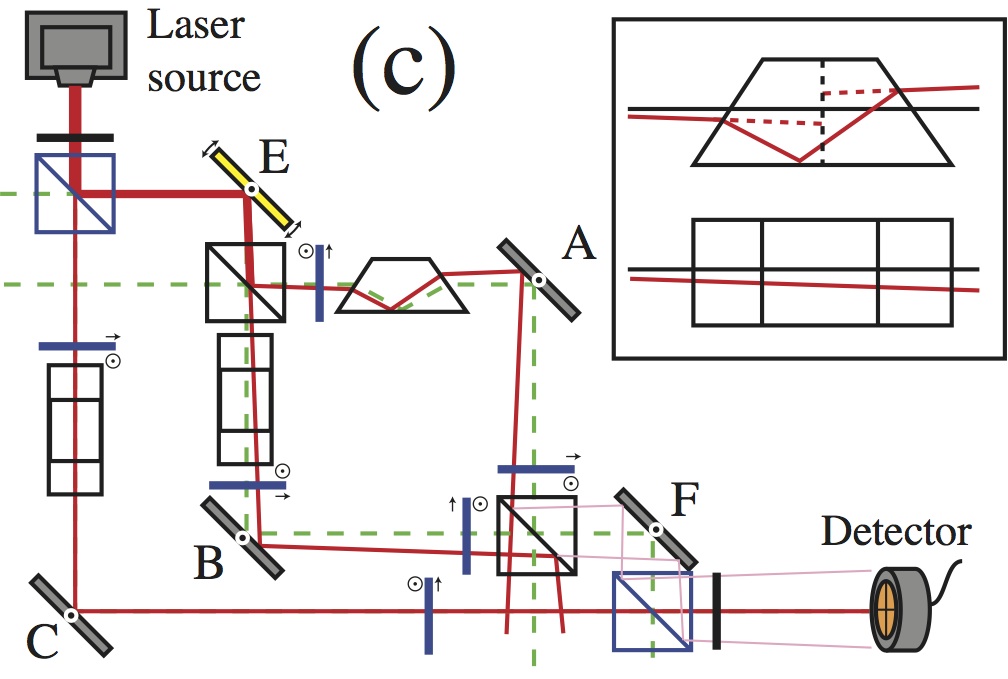
Optical coherence: description and measurement
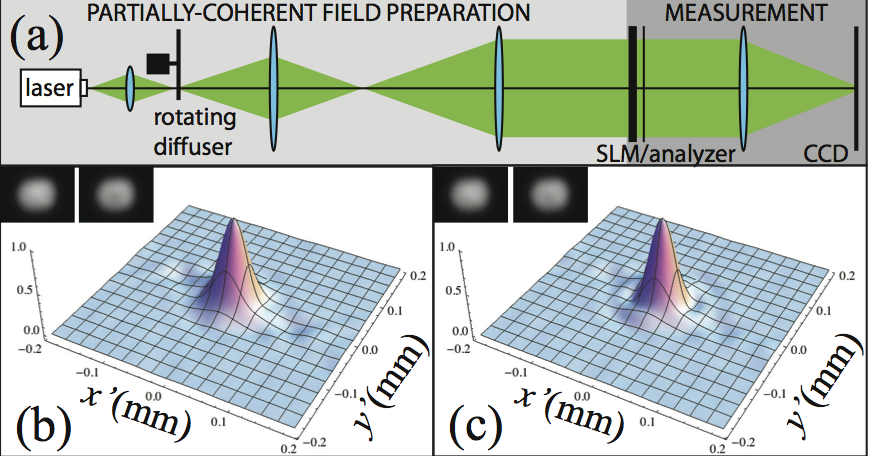
Recent work in our group has focused on simple methods for measuring spatial coherence that do not require wavefront division. In particular, we recently proposed an approach where an obstacle is inserted at the test plane, and the difference of irradiance measurements with and without this obstacle gives access to the spatial coherence at all pairs of points whose centroid is the obstacle’s centroid. Our group has also published theoretical work on the propagation of partially coherent fields. (See also section on Wigner functions.)
See publications on this topic.
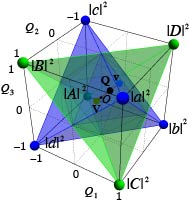
Quantum entanglement and quantum physics
This includes work in quantum physics, such as measures of quantum entanglement, as well as other aspects of the description of wave fields, such as series expansions.
See publications on this topic.
Optical Systems
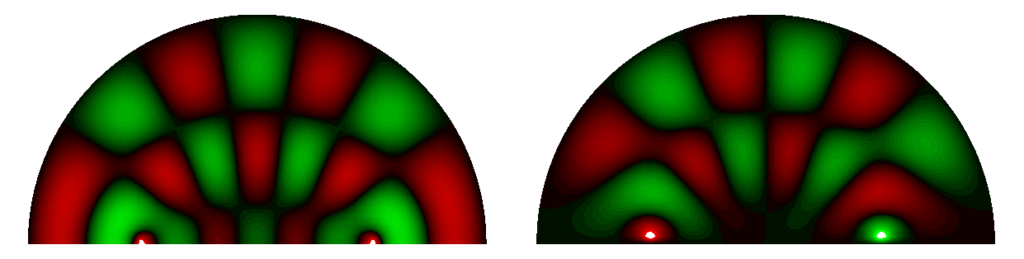
Measures of performance of standard and freeform optical systems. Studies on exotic systems such as Maxwell fish eye lenses and refractive metasurfaces.
See publications on this topic.