Nonlinear Interactions of Classical Light to Mimic a Quantum Interferometer

Quynh Trinh

Mentor

Professor Robert Boyd

Abstract

In quantum N00N state interferometry, the spacing of interference fringes is reduced
by a factor of N, owing to the reduced de Broglie wavelength of the N-photon path-entangled
state, which enables enhanced phase sensitivity. We aim to replicate this fringe halving for N=2 in a nonlinear interferometer using classical light sources and means of detection. While clear interference fringes have not yet been observed—due to insufficient polarization extinction causing signal beam leakage into the idler path—the experiment lays the groundwork for classical analogs to quantum-enhanced measurements. With improvements, the system may enable increased precision over conventional linear interferometers when electronic noise is the dominant source of error.

Background

Interferometry measures optical path differences (OPD) with high precision. In a classical Mach-Zehnder interferometer (MZI), the detected power varies sinusoidally with OPD:

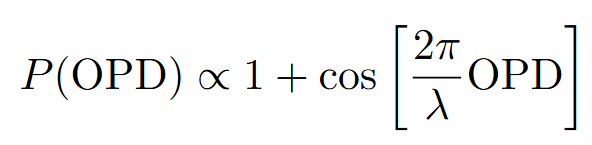
In quantum 2002 state interferometry, where a pair of entangled photons is injected into the MZI input ports, coincidence detection at the outputs varies with twice the OPD [1]:

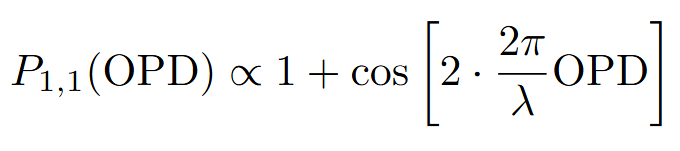
This results in halved fringe spacing compared to the classical case.

Figure 1. Quantum 2002 state interferometry setup from (1). Two identical single photons are incident on the first beam splitter (BS1) and single photons exiting the second (BS2) are detected in coincidence with two detectors. BS1, BS2, and the two mirrors between them form a Mach-Zehnder interferometer with adjustable OPD.

This effect arises from the creation of a quantum N00N state, where N photons exist in a superposition of all being in one path or the other. The “de Broglie wavelength” of light in this state is written as [2]:

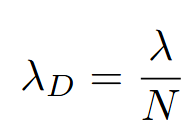
If we consider that the two photons traveling in each arm of the interferometer have an
effective wavelength that is halved, then the halved fringe spacing can be seen as a natural result.

Methods

This project aims to demonstrate a classical interferometer achieving the same halved fringe spacing observed in N00N state interferometry. This can help distinguish genuinely nonclassical features of quantum interference and offers a step toward realizing enhanced sensitivity without the practical challenges of quantum systems.

We built a nonlinear interferometer as a classical analog to a N00N state interferometer. This system is similar to a MZI but uses nonlinear crystals in place of traditional beam splitters [3]. Through double-passing the crystal and phase conjugation in the second difference-frequency generation (DFG) process, the signal and idler beams each acquire twice the phase shift observed in a conventional MZI.

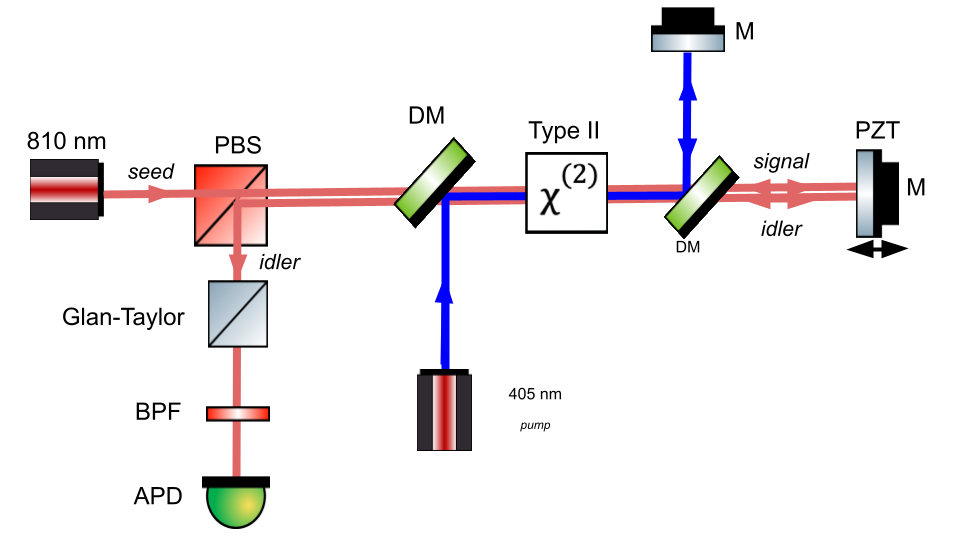
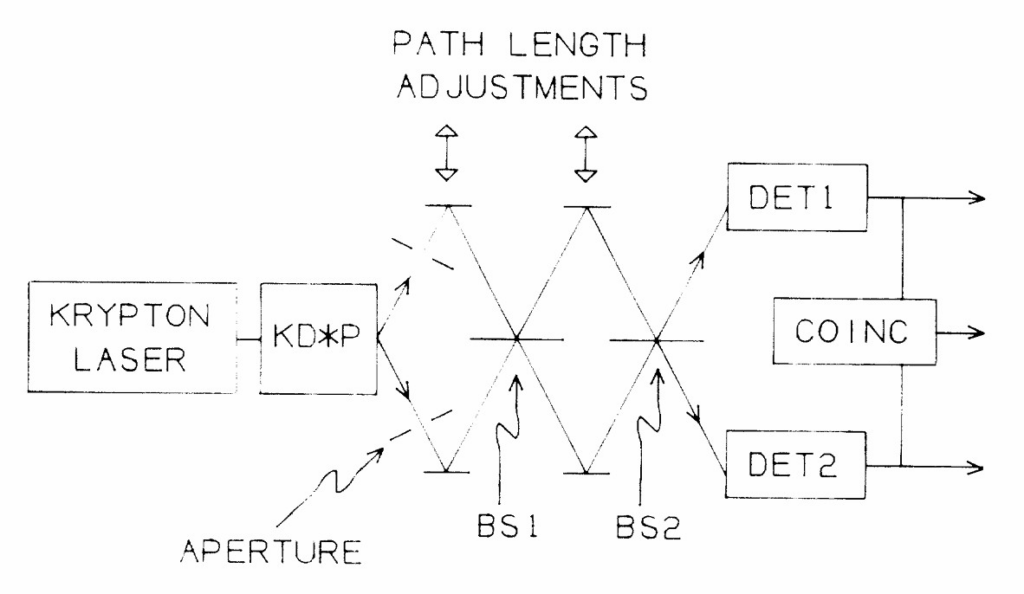
Figure 2. Schematic of the experimental setup. PBS: Polarizing beam splitter. DM: Dichroic mirror. χ(2): Nonlinear crystal. M: Mirror. PZT: Piezo-electrically controlled mirror. BPF: Bandpass filter. APD: Avalanche photodiode.

A simplified layout of the experimental setup is shown in Figure 2. A horizontally polarized 10 mW, 810 nm seed beam and a vertically polarized 50 mW, 405 nm pump beam are combined at a dichroic mirror (DM) after the seed passes through a polarizing beam splitter (PBS). Both beams pass through a Type II nonlinear crystal (left to right), generating an 810 nm idler via DFG. A second DM separates the beams into two arms: the pump reflects off a fixed mirror, while the signal and idler reflect off a piezo-controlled mirror to introduce an OPD. On the return pass (right to left), all beams undergo further amplification in the crystal. After recombination, the idler is isolated at the PBS, filtered with a Glan-Taylor polarizer and bandpass filter, and detected by an avalanche photodiode (APD).

Mathematical Validation

If E_s,in and E_s,out respectively describe the electric fields of the signal wave entering and exiting the nonlinear crystal, and E_i,in and E_i,out respectively describe the electric fields of the idler wave entering and exiting the crystal, the input-output relations for parametric amplification are given by [4]:

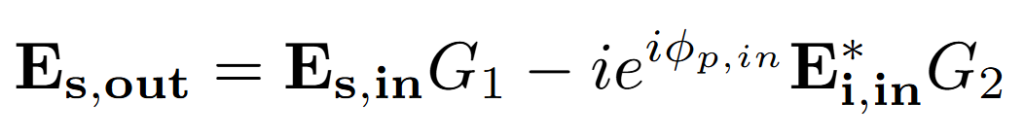
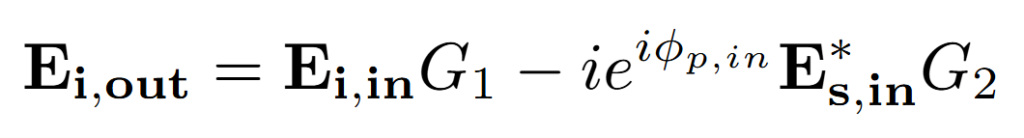
G₁ and G₂ are related to the parametric gain G, which under the approximation of small gain and
plane wave excitation at the crystal [5], is given by:

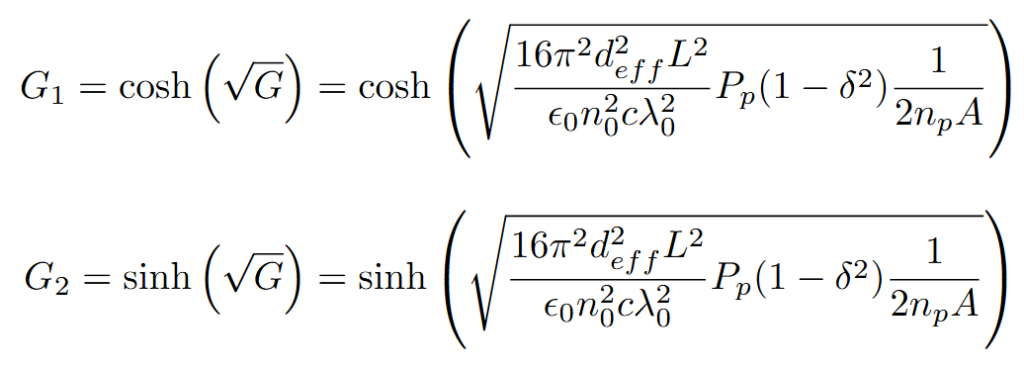
where d_eff is the nonlinear coefficient, L is the crystal length, λ₀ = 2λ_p is the degenerate wavelength, n₀ is the refractive index at degeneracy, P_p is the pump power, δ is the degeneracy factor, n_p is the pump refractive index, and A is the beam area.

Upon entering the first crystal, assume:

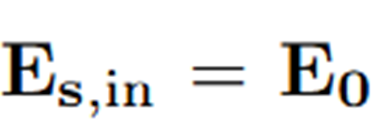
After traveling through the first crystal, the signal and idler fields are given by:

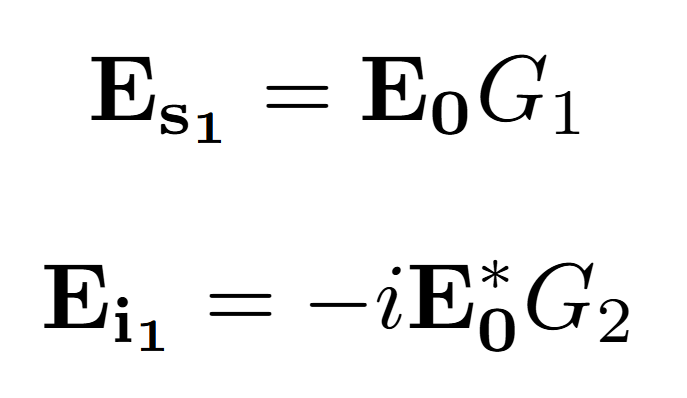
The signal and idler beams each acquire a phase shift ϕ in one arm of the interferometer. After the second pass through the crystal, their fields are given by:

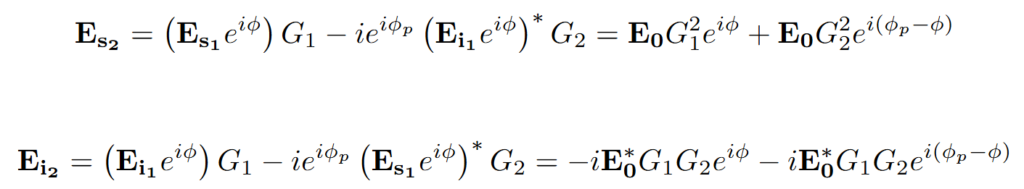
The detected idler intensity varies sinusoidally with twice the phase shift ϕ:

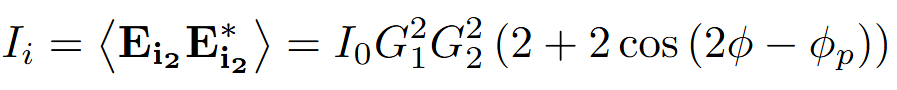
Results

Current experimental efforts have focused on system construction and alignment. We have confirmed correct alignment for spontaneous parametric down-conversion (SPDC) using the 405 nm pump, indicating readiness for DFG generation.

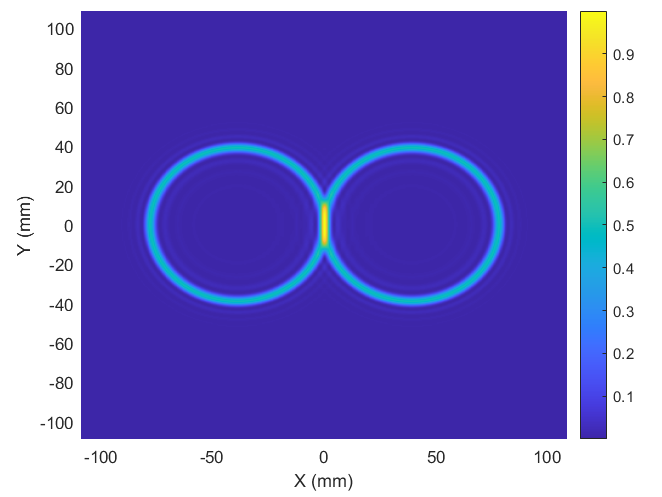
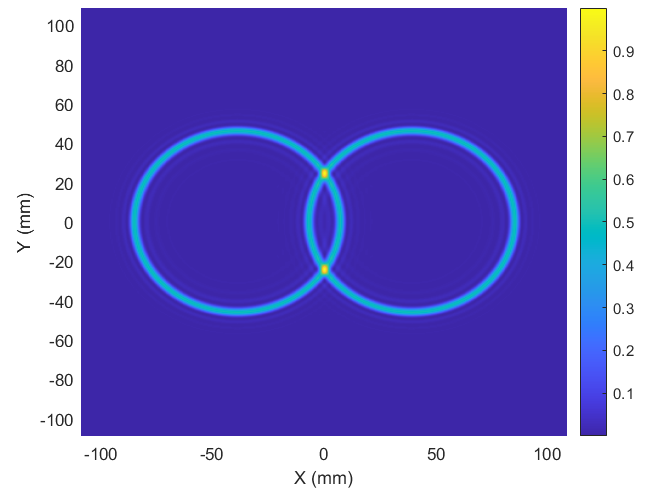
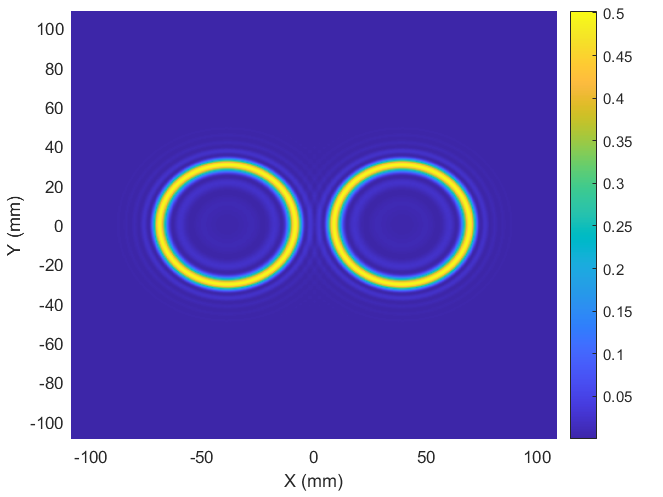
Figure 3. Type II SPDC at different phase-matching angles.
Top row: Simulated emission patterns. Bottom row: Corresponding EM-CCD images.
Left column: Collinear phase-matching.
Middle and right columns: Non-collinear emission at angular deviations from phase-matching.

However, we face challenges observing DFG and reliably detecting the idler due to inadequate signal-idler separation. Currently, polarization filtering is achieved using a PBS (extinction ratio 1,000:1) and a Glan-Taylor polarizer (100,000:1), yielding a combined extinction of 10⁸:1. With a 10 mW seed, this allows ~100 pW of signal leakage to reach the detector. Given our parametric gain G = 1.3×10^-10, the expected idler signal is ~1.3 pW—far below the signal leakage and difficult to resolve.

Figure 4. EM-CCD images after the first crystal pass with polarization filtering using linear polarizers (LP) in front of the camera. Residual signal light remains visible.
Left: 1 LP, no camera gain. Middle: 2 LPs, no camera gain. Right: 2 LPs, low camera gain.

Conclusion

The full interferometer has been constructed, although reliable idler detection remains a challenge due to limited polarization extinction and low parametric gain. Future directions include: (1) using non-degenerate wavelengths to allow spectral separation of signal and idler, (2) employing lock-in amplification with a standard photodiode while tolerating residual signal, or (3) switching to a pulsed pump to boost parametric gain.

References

1. JG Rarity, PR Tapster, E Jakeman, T Larchuk, RA Campos, MC Teich, and BEA Saleh. Two-
photon interference in a Mach-Zehnder interferometer. Physical Review Letters, 65(11):1348, 1990.
2. Joseph Jacobson, Gunnar Bj¨ork, Isaac Chuang, and Yoshihisa Yamamoto. Photonic de Broglie
waves. Physical Review Letters, 74(24):4835, 1995.
3. Jietai Jing, Cunjin Liu, Zhifan Zhou, ZY Ou, and Weiping Zhang. Realization of a nonlinear
interferometer with parametric amplifiers. Applied Physics Letters, 99(1), 2011.
4. Robert W Boyd. Nonlinear Optics. Academic Press, 2020.
5. Richard L. Sutherland. Handbook of Nonlinear Optics. Taylor & Francis, 2003.