iTEST - Senior Design Day

Team

Rachel Chan
Zihao Li
Sinabu Pumulo

Mentor

Brandon Zimmerman

Abstract

The Clear Eye Test is a virtual eye prescription platform that measures refractive error of the eye with a test that can be taken with just a computer, bypassing the need for traditional optometry visits. It aims to:

1) improve the ease and accessibility of eye care

2) provide more personalized prescriptions based on contrast sensitivity

Our team worked on developing algorithms to improve the accuracy of the current platform. We also invited participants to take the test on-site to expand our data size and study the effects of variables—such as room/screen brightness and viewing angle—in a controlled testing condition, with the objective being achievement of clinical accuracy.

Vision

The goal of this project is to optimize the results from the Clear Eye Test using physical optics. These will serve as better informed inputs for the machine learning and visual simulation pipeline in the current platform.

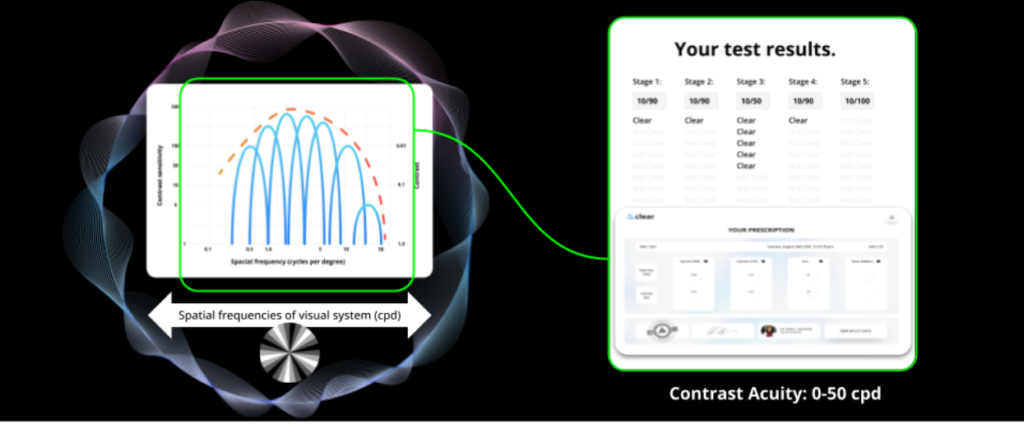
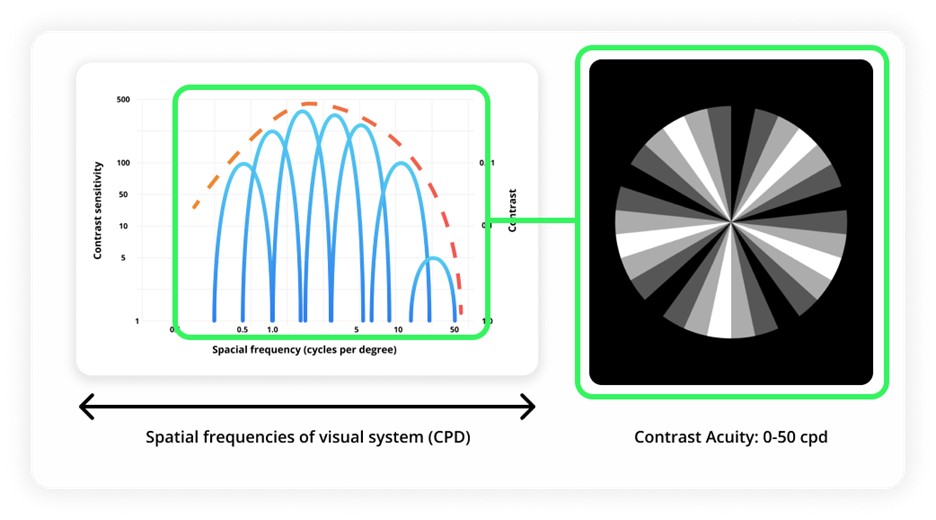
Main factors that affect the initial prescription results include the pupil size, spatial frequency of optotype, and the definition of visual acuity. Taking these into consideration, we aimed to develop an optimization model that can improve the raw prescription estimate using only visual acuity information. To achieve this, the current database is studied and calibrated against clinical 20/20 prescriptions.

Figure 1: diagram of data analysis pipeline to be implemented in the Clear Test platform

Observations

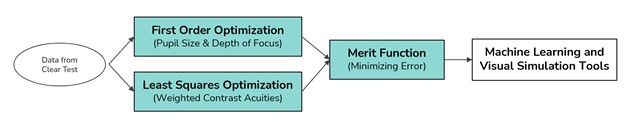
First Order Optimization

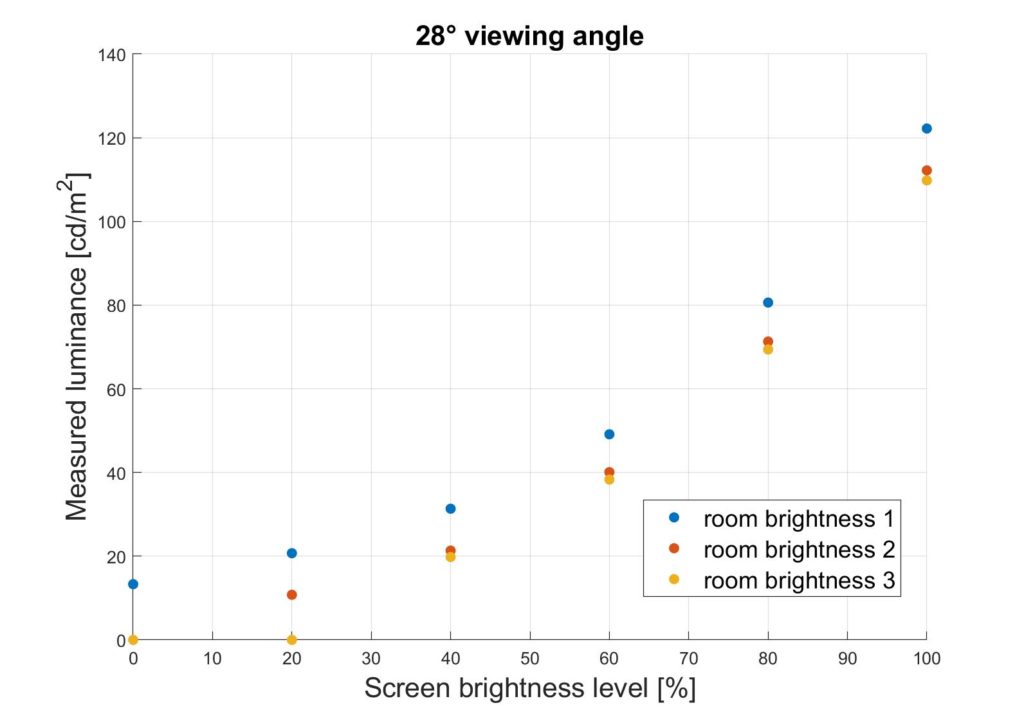
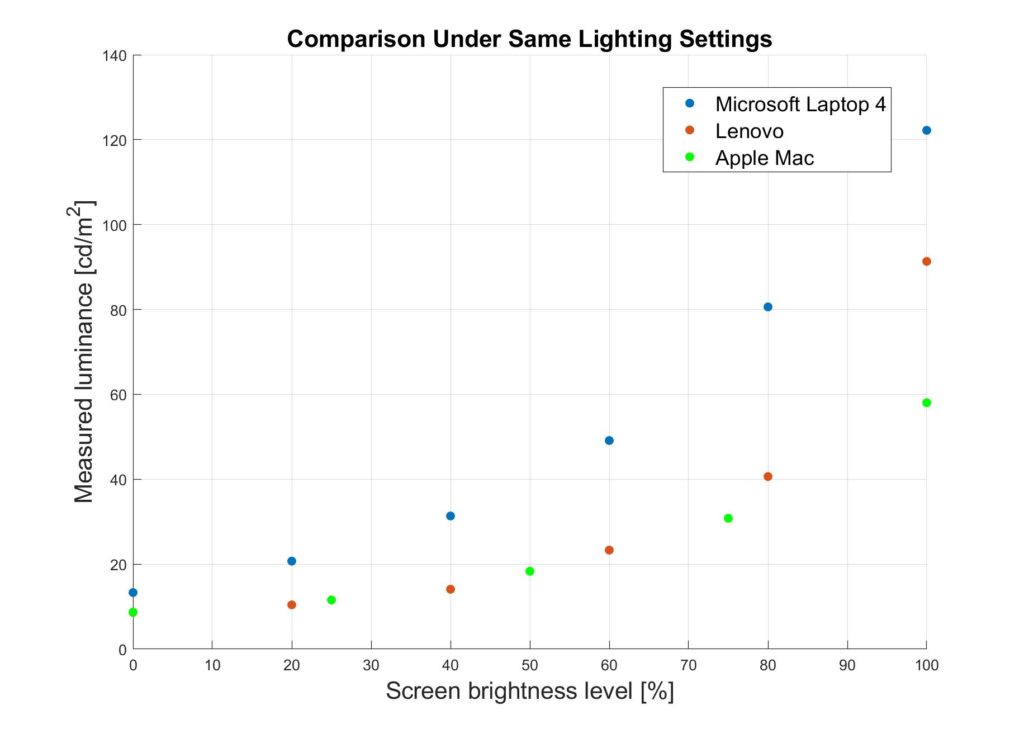
A first order optimization was used to deduce the pupil diameter, which affects the aberrations of the eye, depth of focus, and precision of the initial prescription estimation. This is affected by environmental lighting, monitor brightness, and physiological factors. A preliminary study on the relationship between luminance and pupil diameter was also explored to account for the device-agnostic testing condition.

We found a pre-established mathematical model to express the between pupil diameter of the human eye and the luminance level.

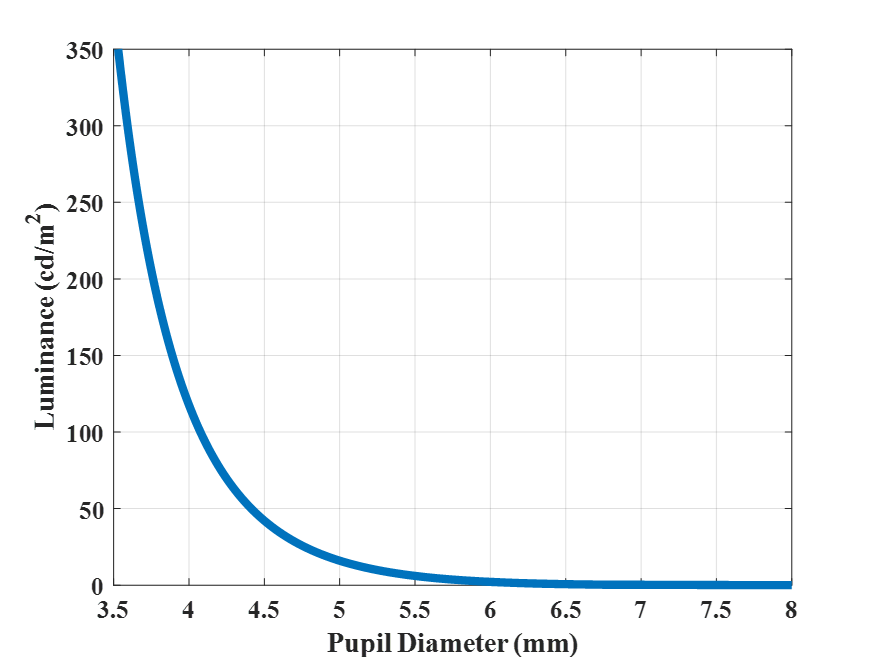
*Figure 2. Luminance value as a function of pupil diameter with 10-degree field of view (without considering age factors).*

Figure 3: (left) contrast sensitivity spans larger range of spatial frequencies of the eye; (right) example of a contrast sensitivity wheel

We modelled the trend of luminance incident on the eye at different combinations of room and monitor brightness with a spectroradiometer.

Figure 4: example plot showing the luminance measurements for a Microsoft Laptop 4; this viewing angle corresponds to a 5’3” height at a distance of 10′ from the computer

Figure 5: for the same brightness combination setting, the luminance measurements were compared for different models. This could serve as motivation for including a calibration factor for different user models.

Least Squares Fit

A least squares optimization routine was used to develop an experimental model that best fit the prescription data using a theoretical relationship between acuity and refractive error. An assumption was made that the visual acuity reading can be decomposed into levels of contrast sensitivity.

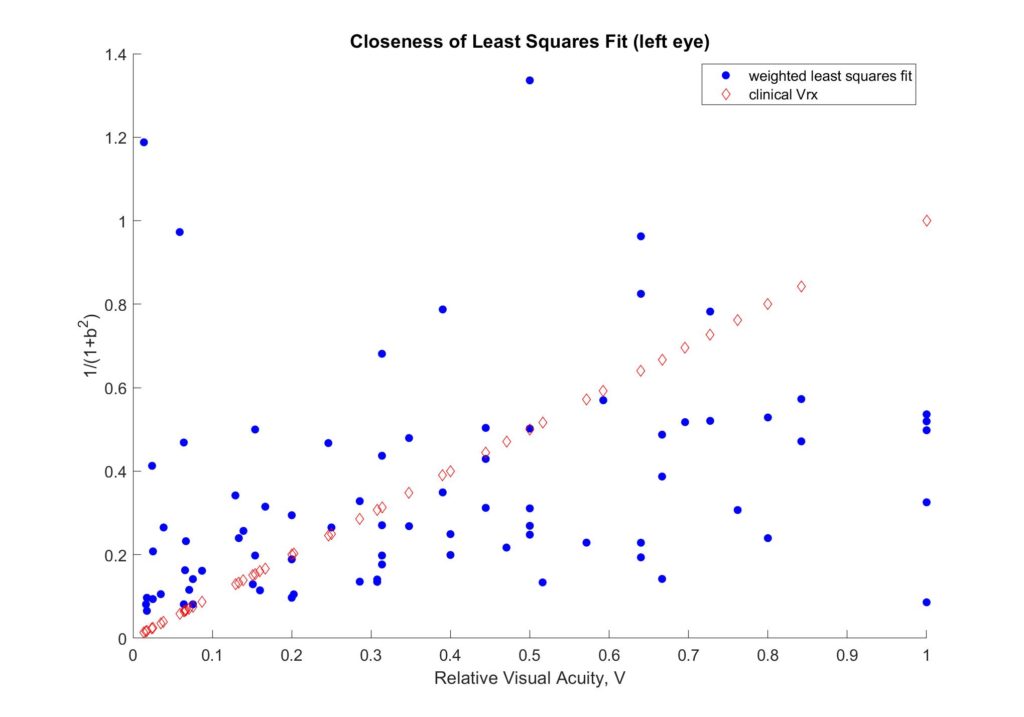
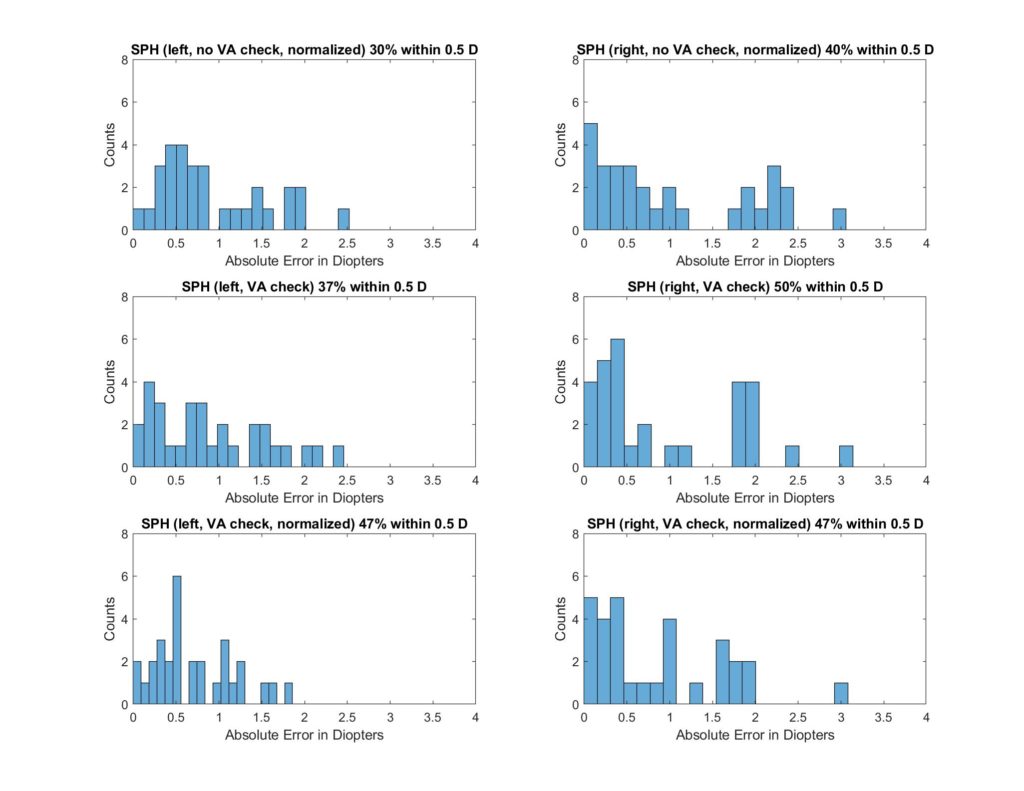
Different approaches were explored to fine-tune the initial assumption. Some limitations that we encountered were visual threshold below which error increases significantly and small training data size. The least squares method is vulnerable to outliers in the data as it will skew the results to compensate for them. The former problem was addressed by preprocessing of the data, and the latter can be ameliorated with more data points. Visual acuity checks were also used to improve the model. The following diagram shows an example of the evolution of accuracy throughout the optimization. The goal is to increase the percentage of SPH and CYL results that are within 0.5 D of clinical prescriptions.

Figure 7: histograms showing the spread of error in SPH and CYL between the optimized values and clinical prescriptions

Merit Function

A merit function incorporated the optimized values–which account for user-dependent variations and used trends from clinical data calibration–to select from a range of best prescriptions for each user.

For each nominal value of the blur quantity, b, a theoretical prescription function is generated. Each data point is then compared to its respective data point from the experimental prescription function to generate an error value. The error values produce an array that can be plotted against the b, giving an error distribution. This error distribution determines the minimum error and, hence, the ideal prescription for the user.

Figure 8: Error distributions for nearsighted patient with a spherical prescription of -2.5 for their left eye.

The accuracy of the prescription picker was then examined for each eye from a database.

Figure 9: The histograms show the absolute error from the merit functions prescription picker.

Left	60.4%
Right	53.1%

Table 1: The table above shows the accuracy of the Merit function’s prescription in a data set that did not include contrast acuity. The result is accurate if within 0.5 diopter of the clinical prescription. This accuracy is expressed as a percentage.

This is the first phase of the project, and incorporation of the other two optimizations has promise to increase this accuracy.

Future Directions

The optimization routines will be synergized for an improved prescription estimate and integrated into the current Clear platform. The merit function by itself can achieve an accuracy of < 0.5 D up to 64% of the time. The least squares fit has also proven to optimize prescription selection by up to 13%.

Through the initial attempts at developing an optimization pipeline to improve the accuracy of the prescription estimate, we noted few important trends that should be further studied.

Increase data size: the convergence of the least-squares optimization is heavily dependent on the characteristics in the training data set. Running it across the whole population might be too general to extract any useful trends. For reliable conclusions to be made, further attempts on optimizing for different demographics (e.g., age, severity of refractive error, etc.) could yield promising trends.
Incorporate eye models: we noted the assumption that the refractive error comes solely from the cornea, which is only part of the picture, as there can be variation from depth of focus, axial length, and accommodation. This could possibly bring up the maximum accuracy that we can reach with these methods.
Optimize by axis of astigmatism: it was noted throughout the development process that the cylinder values do not respond as well to the blur quantity for refractive error. Further work can be done on improving the contrast optotypes for astigmatism and to separate the users based on their axis of astigmatism.
Explore new contrast sensitivity models: the current method is based on an established relationship between refractive error and visual acuity, but there might be an improved model that includes the role of contrast sensitivity.