Team
- Chang Liu, B.S. Optical Engineering ’23
- Angel Paz, B.S. Optical Engineering ’23
- Matthew Scibilia, B.S. Optical Engineering ’23
Customer

Customer Primary COntact
- Dr. Leonard Zheleznyak
Project Advisor
- Dr. Susana Marcos, University of Rochester
Abstract
The Myopia Control with Optical Design project is a senior design project that consists of the development of ray-tracing models of an emmetropic, hyperopic, and myopic human eye in Zemax OpticStudio for evaluating diffractive-refractive hybrid contact lens designs. The project’s specifications, features, and design considerations were based on input from Dr. Len Zheleznyak of Clerio Vision and Dr. Susana Marcos of the University of Rochester. The project aims to produce an accurate and representative model of the human eye and integrate lens design models of contact lenses from Clerio Vision to compare and analyze their performance in correcting wavefront errors in the eye. The project’s ultimate goal is to apply this technology to school-aged children with the objective of slowing the development of myopia. It is additionally possible that results from the model analyses can be used to develop contact lenses that achromatize the eye by eliminating both longitudinal chromatic aberration (LCA) and transverse chromatic aberration (TCA). The models allow for the analysis of the polychromatic point spread function, through-focus image quality, and chromatic aberrations at different retinal positions corresponding to a range of input ray angles across the horizontal meridian of the horizontal binocular field of view of the eye.
Description
This project was comprised of multiple sub-objectives aimed at Zemax modeling and analysis, which were established, pursued, and systematically accomplished throughout the design process.
built-in Zemax Eye model evaluation
The first of the primary sub-objectives entailed in this project was to conduct a comparative analysis between the performance of the built-in eye model included in a standard Zemax OpticStudio license and the retinal aberration data published in a 2020 Clinical and Experimental Optometry article authored by Dmitry Romashchenko, Robert Rosén, and Linda Lundström. This article presented consolidated aberration data from over 2400 studied eyes, which was reviewed to deduce the “average” performance of the human eye. The Zernike terms representing these aberrations were then juxtaposed with those generated by the Zemax built-in eye model. Our analysis revealed that the Zemax model fell short of presenting a representation of the true human eye’s performance, as it made several oversimplifications.
This evaluation served to substantiate our endeavor to produce a better model, one that may not necessarily incorporate every complex eye surface and material structure as they exist in reality, but one that performs in accordance with the data obtained from the clinical study.
improved eye models
Our initial approach to optimizing the eye model provided by Zemax to match our desired retinal aberrations involved building a merit function that set weighted goals on each Zernike term of interest while varying the surfaces present in the eye model to achieve the desired outcome. The curvatures, asphericities, and thicknesses of each surface in the default model were constrained to remain reasonable and “eye-like”. However, we discovered that this method of optimization was insufficient for reproducing the aberrations that we required in the model. The optimizer lacked enough degrees of freedom to achieve close replication of many of the aberrations simultaneously, and it was unable to model several, such as oblique astigmatism, entirely due to the forced preservation of axial symmetry in the default model. After discussing with Dr. Zheleznyak, we shifted to our secondary plan of placing a Zernike Phase Surface in the iris of the eye to “cancel” the incorrect aberrations of the Zemax eye model and induce the aberrations that we sought on the retina. Using the Zernike Phase Surface, we created a series of Zemax models for each field angle of the myopic, emmetropic, and hyperopic eyes that represent the behavior and performance of the real human eye without the need for an accurate GRIN crystalline lens, correct retinal curvature, or precise thicknesses of eye components.
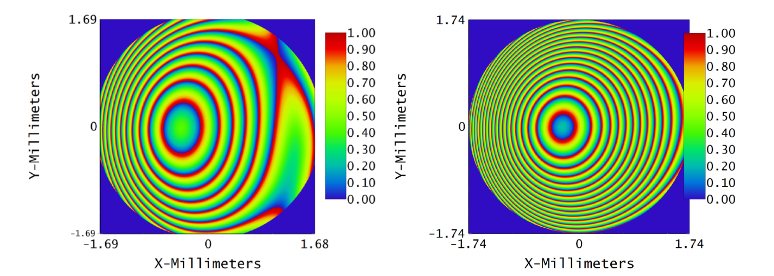
We optimized the Zernike Phase Surface in each Zemax file such that it induced the precise aberrations required to correct the Zemax eye model and introduce the desired terms to represent real eye data. This allowed the Zernike terms modeled to match those that are desired down to a millionth wave or less difference in each Zernike term. Ultimately, the shell of the Zemax eye model was left in place to maintain the imagery of the eye, while the optimized Zernike Phase Surface excelled at using the desired final aberrations to induce the correct phase delays and produce the result we were seeking.

Diffractive-Refractive hybrid contact lens
To create the contact lens, a 4.7-diopter diffractive-refractive hybrid contact lens was modeled and added to the emmetropic, myopic, and hyperopic eye models for each field angle. The contact lens is 100 µm thick, has an 8mm diameter optic zone, and is composed of silicone hydrogel for precise fitting on the cornea. The contact lens is designed to correct for LCA, which contributes to the development of refractive errors on the periphery. The hybrid lens has three surfaces, with the mid surface being the diffractive element that has a phase delay profile resembling the surface shape of a fresnel lens. The diffractive element introduces negative LCA by nature, compensating for the positive LCA induced by other refractive elements in the eye system. The contact lens has a base refractive power of 1 diopter and a diffractive power of 3.7 diopters on the internal diffractive surface. The modeled diffractive surface induces an optimized phase change across the wavefront that determines the surface power, which can be re-calculated for any new design.
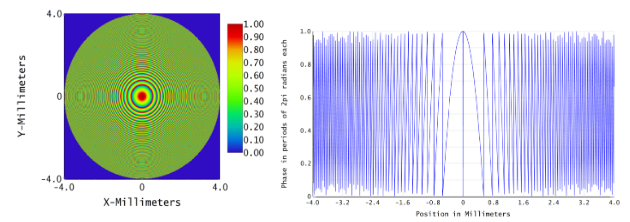
The fresnel-shaped diffractive surface inside the base contact lens was implemented to modify the phase profile of the incoming beam to simulate the diffractive power of the contact lens. The number of Fresnel rings is related to the wavelength, the radius of the aperture, and the distance of the screen from the aperture by the Fresnel Number equation. After computing the expected number of phase change zones on the diffractive surface to achieve the desired 3.7 diopter power, the diffractive surface was optimized in Zemax to match the power that was sought. With the surface phase analysis, it was verified that the diffractive surface was inducing 53.3 waves of defocus as planned and calculated with the Fresnel Number equation.
Contact Lens Evaluation and Results
The addition of a diffractive-refractive contact lens to the eye models initially results in decreased performance compared to the bare initial model. This is because the contact lens introduces 4.7 diopters of defocus to the well-focused eye models. To analyze the effect on the performance and chromatic aberrations of the eye models, the models must be refocused to emulate the muscular refocus of the human eye when looking through a corrective contact lens. Rather than varying any surface of the eye model, the refocus was accomplished by varying the object position from infinity to a finite conjugate. The finite object distance was optimized to be between 150 and 200 mm from the first surface of the contact lens to allow for refocusing without altering the model surfaces themselves. The refocused systems show slightly better performance than the original eye models when evaluating the polychromatic point spread function in terms of spot size, but it is unclear if this performance is a true representation of the eye’s refocused performance with a hybrid contact lens.
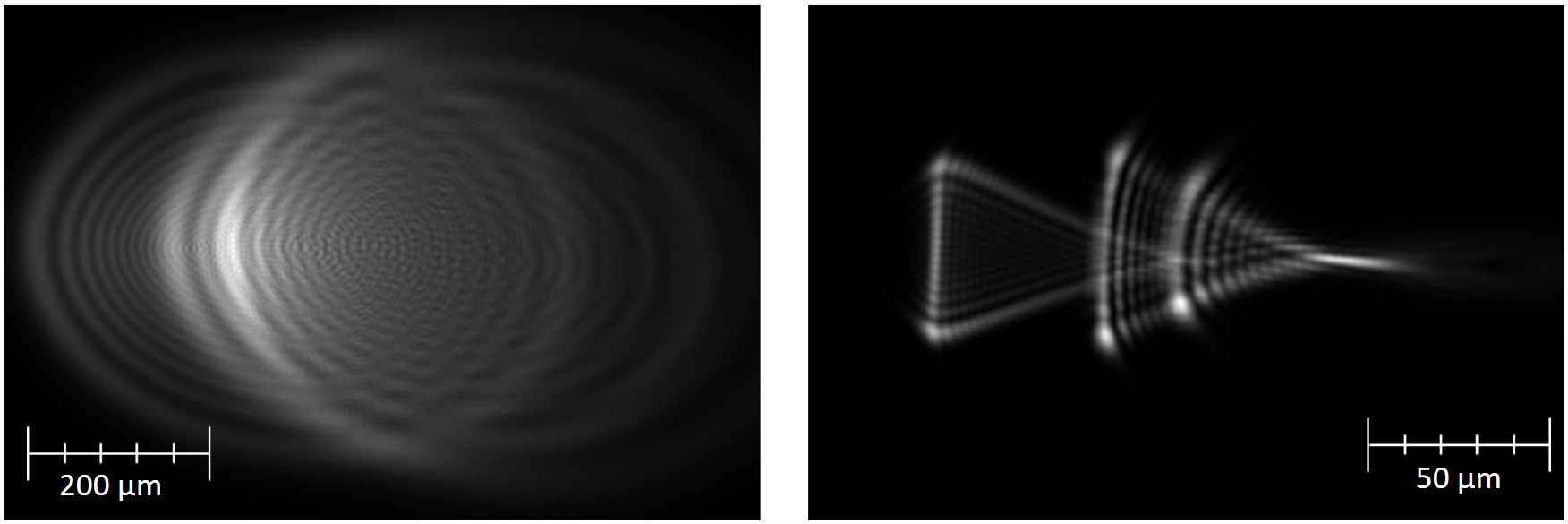
We also conducted an analysis to study the impact of diffractive-refractive contact lenses on the chromatic aberrations present in eye models. The goal of the design was to reduce longitudinal chromatic aberration to zero by introducing negative LCA using the 3.7 diopter diffractive surface, which was also expected to reduce the magnitude of transverse chromatic aberration. The evaluation of the chromatic aberrations present in the eye models revealed that LCA was reduced by over 76% from a maximum difference in focus position across visible wavelengths of 673 um in the bare eye models to only 160 um in the models that included the hybrid contact lens.
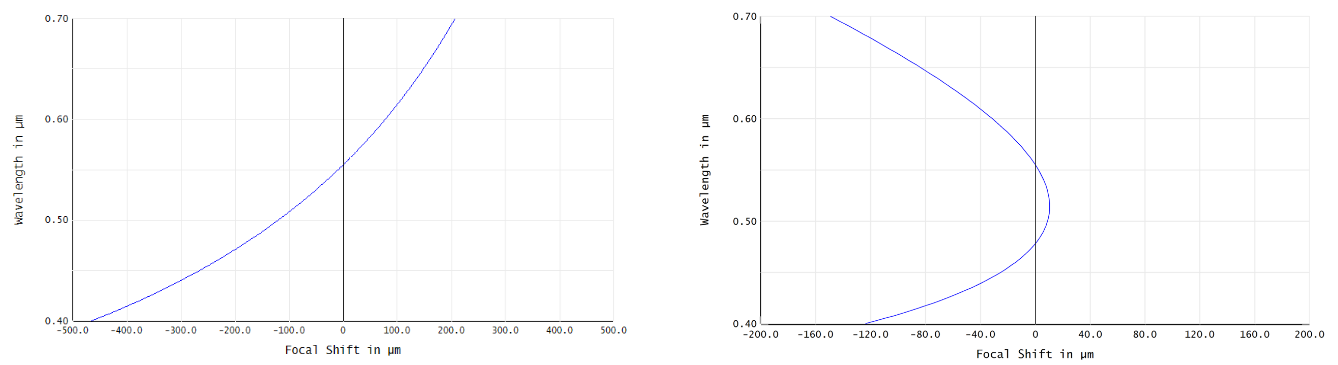
However, the addition of the contact lens almost doubled the magnitude of TCA, which was unexpected. This finding will inform future research into the development of diffractive-refractive hybrid contact lenses by exploring the relationship between longitudinal and transverse color correction and seeking to correct both simultaneously.
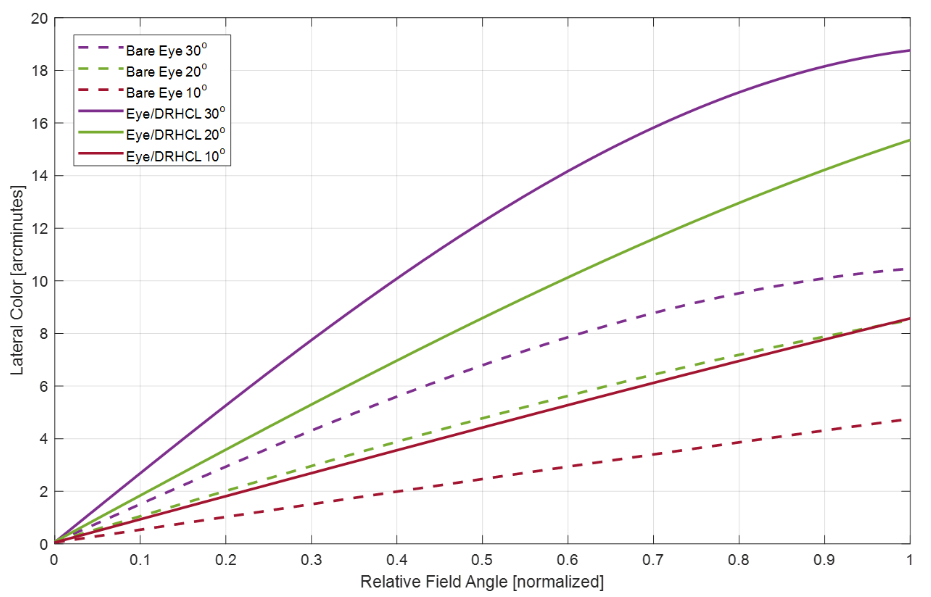
Despite this unexpected result, the eye models provide Clerio Vision with a strong foundation for studying the impact of the 4.7 diopter lens on the performance and chromatic aberration of emmetropic, myopic, and hyperopic eyes. Future work will include developing new contact lens designs and testing their simulated performance using our series of eye models, which we have provided to Clerio Vision as our project deliverables.
