Nonlinear Propagation of Volumetrically Full Poincaré Beams

“Engineering is about turning ideas into reality. The senior design project is an opportunity to take the theoretical and make something practical. This experience will carry you into the future and you will be better for it.”

—Mr. Collins S. Yawe (BS 2021, Chemical Engineering)

Tatsunosuke Hanano

Mentor

Professor Robert Boyd

Abstract

Light with structured polarization is called polarization structured beams, and they have gotten attention because of their ability to process more information per photon than ordinary light [1]. Moreover, recent research showed that polarization structured beams resist the self-focusing effect through nonlinear propagation more than ordinary light [2]. Volumetrically full Poincaré (VFP) beams are also one of polarization structured beams. In this research, we investigated the stability of VFP beams under nonlinear propagation.

Background

Poincaré sphere is a way of representing the polarization state using the Stokes parameters [3].

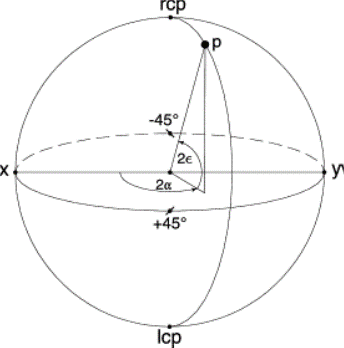
Figure 1: Poincare sphere [3]. x, and y represent horizontal and vertical polarization,
+45 and -45 denote diagonal and antidiagonal polarization, and rcp and lcp are right- and left-circular polarization, respectively [3]. The other points that are not on the coordinate axes represent elliptical polarization [3].

FP beams have a polarization distribution covering the surface of the Poincaré sphere [4], and FP beams can be created by the superposition of two Laguerre-Gauss beams. VFP beams have polarization distribution covering the surface and filling the interior of the Poincaré sphere [4]. VFP beams are made from the superposition of temporally incoherent FP beams with opposite helicity [4,5].

The refractive index of a Kerr-type nonlinear material is dependent on the intensity of light [6]. The focusing of the beam due to the increased refractive index of the material is called self-focusing [7]. The stabilities of different types of beams under self-focusing can be compared from intensity statistics of the beams after propagating nonlinear media.

Result

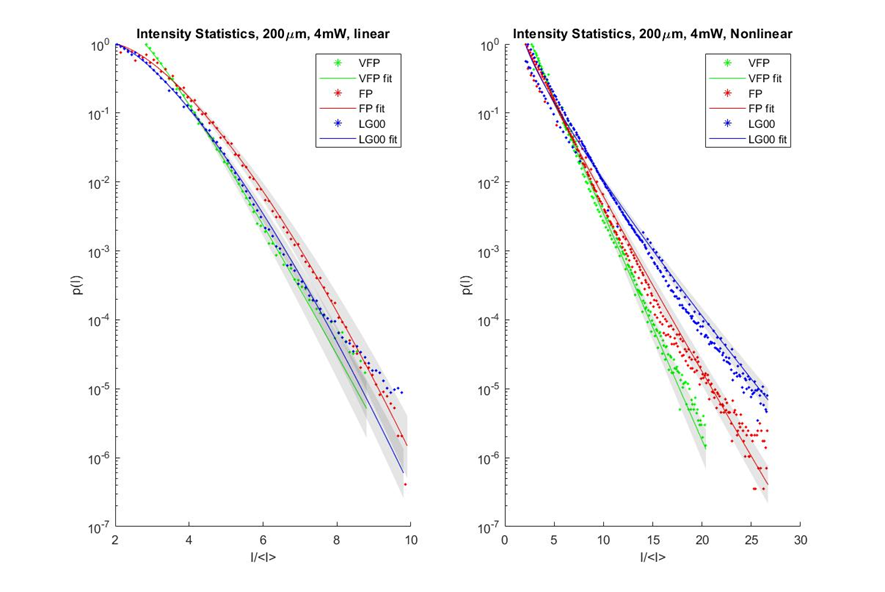
Figure 2: Intensity Statistics (power: 4mW, correlation length: 200um), shaded area is uncertainty, left: linear propagation, right: nonlinear propagation

We propagated VFP beams, FP beams, and LG00 beams through Rubidium vapor for nonlinear propagation and air for linear propagation. Then, the intensity statistics of VFP beams, FP beams, and LG00 beams were measured after nonlinear propagation and linear propagation. The intensity statistics under linear propagation are almost identical for all beams. However, for nonlinear propagation, the intensity statistics of LG00 beams deviated most from the intensity statistics of linear propagation, and the intensity statistics of FP beams deviated from the intensity statistics of linear propagation more than the intensity statistics of VFP beam did. Thus, we could observe that VFP beams were more stable than FP and LG00 beams.

Reference

[1] H. Rubinsztein-Dunlop, A. Forbes, M. V. Berry, et al., “Roadmap on structured light,” J. Opt. 19, 013001 (2016).

[2] A.N. Black, S. Choudhary, E.S. Arroyo-Rivera, H. Woodworth, and R.W. Boyd, “Suppression of Nonlinear Optical Rogue Wave Formation Using Polarization-Structured Beams,” Phys. Rev. Lett. 129, 133902 (2022).

[3] K. Rochford, “Polarization and Polarimetry,” Encyclopedia of Physical Science and Technology (Third Edition), R.A. Meyers Ed, (Academic Press, San Diego, 2002), pp. 535-536.

[4] A. M. Beckley, T. G. Brown, and M. A. Alonso, “Full Poincaré beams ii: partial polarization,” Opt. Express 20, 9357–9362 (2012).

[5] A. N. Black and R. W. Boyd, “Generation of volumetrically full Poincaré beams,” Opt. Soc. Am. A 39, C161-C166 (2022).

[6] R.W. Boyd, Nonlinear Optics, 4th ed. (Academic Press is an imprint of Elsevier, San Diego, 2020), Chap. 4, pp. 203-204

[7] R.Y. Chiao, T.K. Gustafson, and P.L. Kelly, “Self-Focusing of Optical Beam,” Phys. Rev. Lett. 15, 1005. (1965)