Antony Georgiadis
Mentors
Professor James Fienup and Joseph Tang
Abstract
Wavefront sensing via phase retrieval algorithms are critical to enabling the use of large aperture systems on the ground and in space as they allow users to get nanometer measurements of alignment errors without the need of another instrument like an interferometer. During the development process of new phase retrieval and other alignment algorithms it can be highly important to test on a physical system to verify the validity of the algorithms. The use of full-scale telescopes is unwieldy and make for a costly verification process, whereas small-scale models offer an alternative that is much more accessible. The addition of precision manufactured pupils and alignment of these pupils will allow for further exploration of systems that use slightly different geometries without having to purchase new MEMS devices or build larger scale models that would otherwise inhibit the rate of algorithm testing. In this thesis this is explored by replicating the pupil of the James Webb Space Telescope.
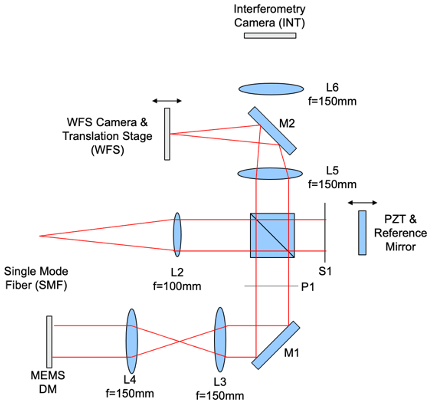
MEMS System
The MEMS System consists of a single mode fiber that is collimated, which is representative of a point star, a wavefront sensing camera that is on a translation stage for performing focus diverse phase retrieval, a phase shifting interferometer system for verification and a Micro Electro-Mechanical System (MEMS) mirror consisting of 37 hexagonal segments that can be individually adjusted for Tip/Tilt and Piston. This system is used to generate real world data and test the performance of phase retrieval algorithms.
The original system has a circular aperture that would help block out undesired mirror segments. However, the extra segments are clearly not completely blocked, and struts are not represented as on the real telescope. The goal is to improve this by limiting the aperture to just the hexagons of interest, in addition to adding struts.
Phase Retrieval
Light propagates through space as an electromagnetic wave and can be decomposed into an intensity component and a phase component. When we measure light with a detector like a CMOS or CCD array, we are only measuring the intensity or energy in the beam. For alignment purposes we would like to know the phase of the object, since the phase of the object is proportional to alignment error. Phase retrieval allows the user to take a traditional image which measures intensity and take advantage of known features about this image (e.g., aperture shape) in order retrieve this additional missing phase information.
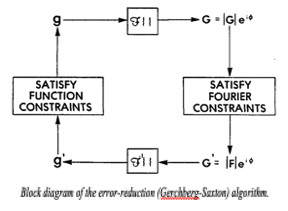
Focus diverse phase retrieval for wavefront reconstruction is a special type of phase retrieval used for measuring aberrations in an optical system. It takes advantage of the way a wavefront changes through space as it propagates through focus to allow for more robust reconstruction. The process generally consists of first predicting a Zernike or other error in the pupil plane, propagating it to the different defocus planes, comparing that to measured intensity at each plane and then adjusting the prediction. In order to make those adjustments a non-linear optimization algorithm is used in conjunction with an error metric which also allows the algorithm to evaluate its progress.
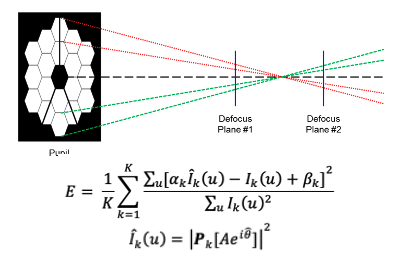
Addition of the Pupil Mask
In order to create a new mask a CAD model was created that consisted of many hexagonal segments and struts that could be easily manipulated and traced to create masks of various shapes and sizes.
The magnification of conjugate planes could be changed to tallow for larger masks that are easier to manufacture. However, a critical aspect to understand is how the change in magnification will impact the sampling ratio (Q-Factor) of the system. In order to perform phase retrieval generally a Q-Factor of 2 or more is required so when magnifying the pupil by changing the focal length of L4 the F/# of the imaging system needs to changed accordingly to compensate.

Once a design was created various materials were attempted to be fabricated at two different magnifications. Those included SLA 3D printing, Chrome on Glass and laser cut steel. Only the first two came in time for testing. The 3D printed plastic clearly has features that are far too par as shown above however the chrome on glass appears to perform quite well despite worried about reflections from the surface interfering with the measurements in the system. Testing of the final pupil mask in the system is still ongoing.
Algorithm Comparison
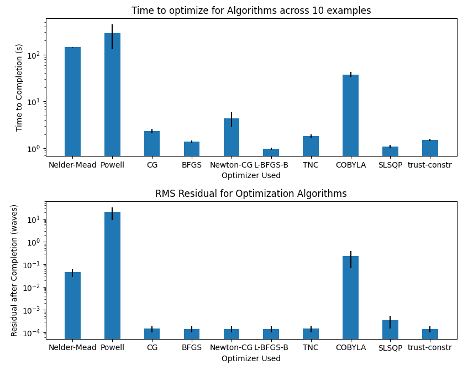
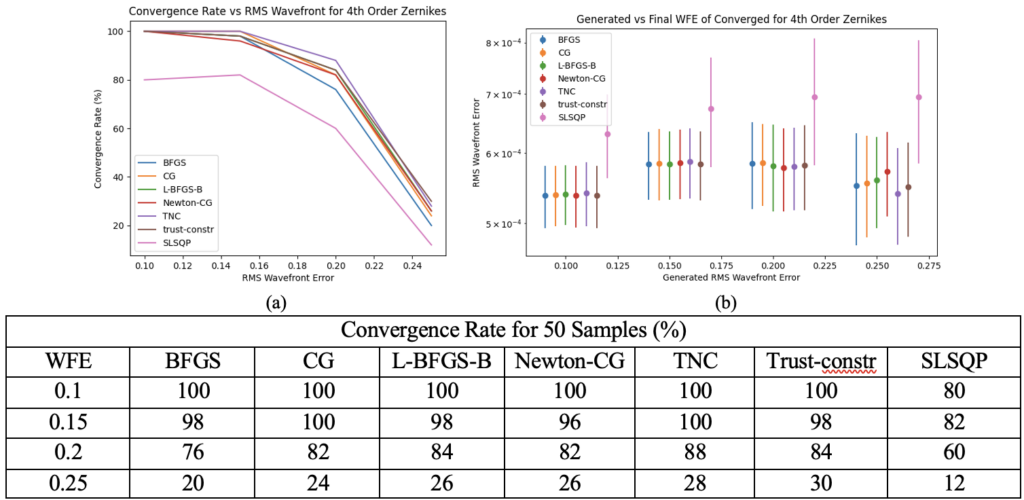
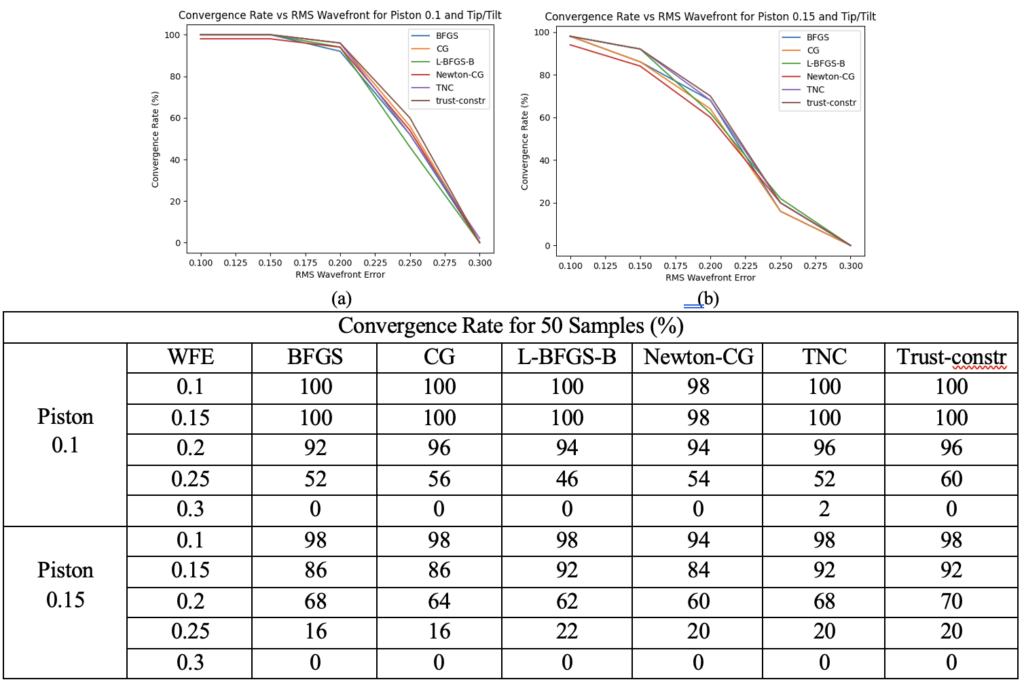
The next portion of the project was to test out various non-linear optimizers which are used for retrieving the wavefront space from the Scipy.minimize library. During this process an initial set of piston only data was generated and retrieved to eliminate the worst algorithms on a smaller set. Then a set of data through 4th order zernikes was analyzed followed by a Piston/Tip/Tilt set that is representative of the departures that the MEMS system can make. The results of that analysis can be seen below.
Conclusions
During this project a system for fabricating pupils to work with MEMS devices for phase retrieval was generated and tested. The optimal material for creating this pupils currently appears to be chrome on glass due to it’s shorter lead times however, it should be noted that a slight tilt of the mask is required to eliminate reflections from going through the system. From the algorithm analysis it was found that L-BFGS is the best algorithm available in the Scipy.minimize library which aligns with what the group had previously found.
Acknowledgments
Thank you to Prof. Fienup and Joseph Tang for their help and guidance on this project as well as to Jennifer Krushwitz, Ed Herger and James Alkins for their assistance in sourcing parts and fixing old components.