Author
Kagan Yanik
Mentor
Andrew Jordan
Abstract
We discuss the thermodynamic aspects of a single qubit based device, powered by weak quantum measurements, and feedback controlled by a quantum Maxwell’s demon. We discuss both discrete and continuous operation of the measurement based device at finite temperature of the reservoir. In the discrete example where a demon acquires information via discrete weak measurements, we find that the extracted work as well as the entropy production is completely determined by a measure of the quantum measurement arrow of time. We also discuss a realistic time-continuous operation of the device where the feedback is applied after a sequence of weak measurements. We derive the exact finite-time probability distributions of work and entropy along individual quantum trajectories of the quantum measurement process, and relate them to quantum measurement arrow of time. We then aim to derive the exact finite-time probability distributions of work and entropy for the same engine that is powered by simultaneous weak quantum measurements.
Background
Measurement fueled engines consist of a system (a single particle/qubit), an observer/Maxwell’s demon that applies measurements and a feedback protocol that depends the measurement outcome.
Weak measurements are realized by weakly coupling a measurement apparatus to a system. Instead of collapsing the wavefunction of the qubit, a weak measurement partially collapses the wavefunction such that the Bloch vector points to a mixed state (inside the sphere) and after this measurement we do not know which state the system is in exactly, although we might know more about which state it is possibly in than before the measurement.
The arrow of time deals with the emergence of irreversibility from time-reversal symmetric dynamical laws: the dynamical equations of physics are time-reversal symmetric, while ensembles of physical systems pick out configurations that prefer an increase in entropy, or a preferred arrow of time. Nevertheless, the time symmetry of dynamical equations also implies that if we repeat an experiment sufficiently many times, we might be able to record statistically rare events where the state of the system reverts to its initial conditions
We have established that weak measurements cannot collapse a wavefunction and we cannot gain full information about the state of the system. Moreover, if we first apply a weak quantum measurement to a system and then we apply another weak measurement we have a chance to undo the previous measurement if we measure in opposite direction. This means that we returned to our initial state before the measurements and the process is reversible.
Methods
Single Type Weak Measurements
We develop this research in two stages: at first stage we describe a system that consists of a qubit that is weakly-coupled to a hot thermal reservoir that thermalizes the qubit consistently to keep it in a steady state via heat exchange. In the first stage, we apply a discrete weak measurement along the x-observable and then apply feedback to extract work from the qubit. At the second stage, we apply a sequence of continuous weak measurements and apply a feedback at the end to extract work from the engine.
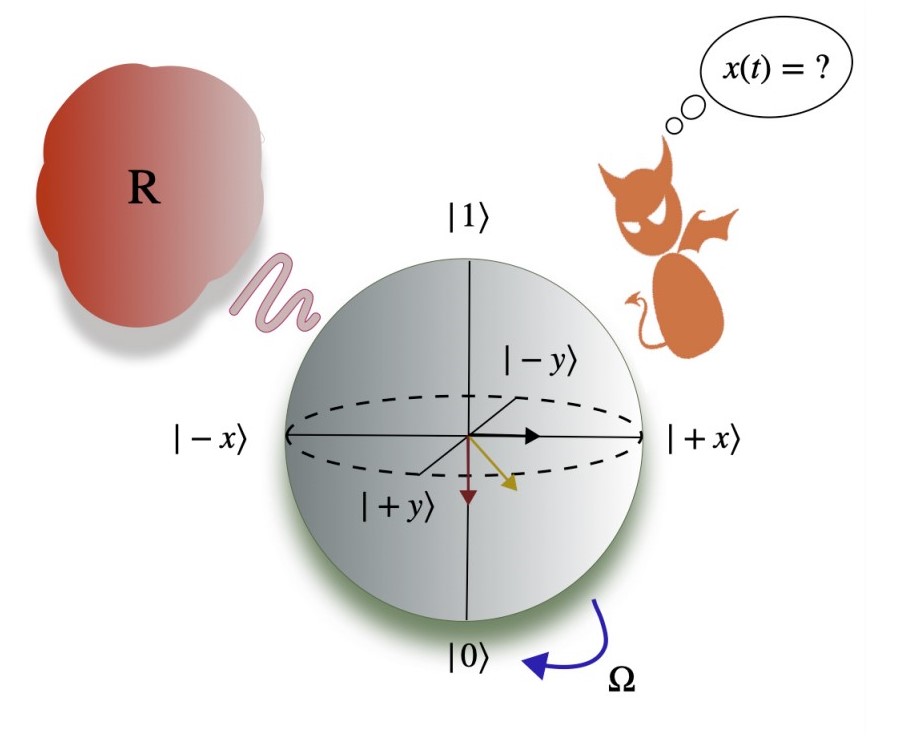
Simultaneous Weak Measurements
We then use the same setup with the continuous measurement case, but now apply measurements along x and z observables simultaneously.
Results
Single Type Weak Measurements
We have seen that as measurements get stronger, we are more certain about the time direction of the evolution of our system and we are able to extract more work and reduce the entropy more.
For continuous measurements, we have done 20,000 simulations and obtained finite-time statistics of work extraction and entropy for a practical engine.
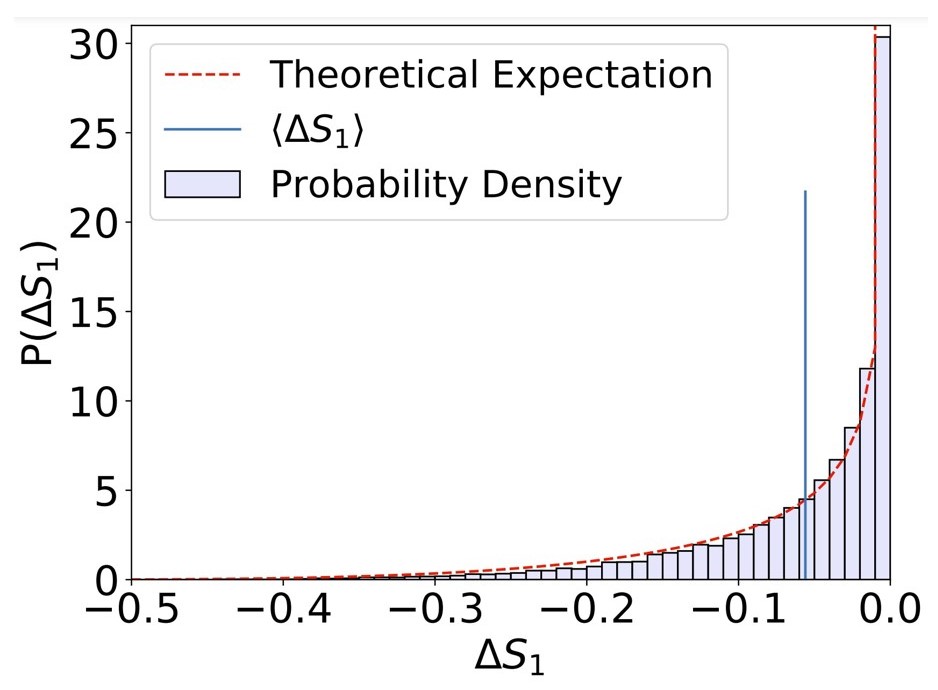
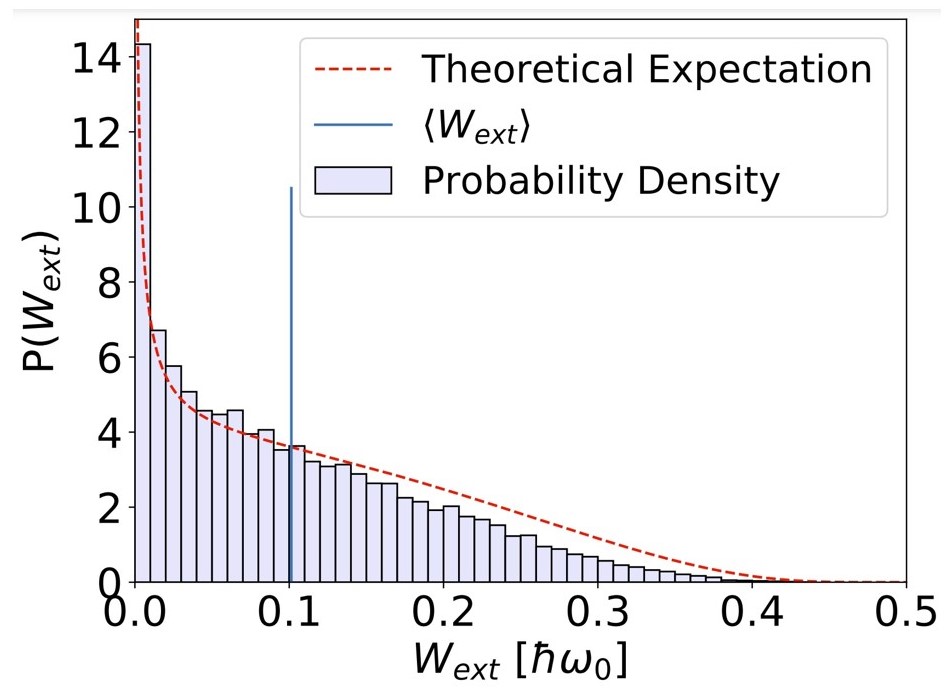
We saw that the highest probability of change in entropy of the qubit and work extraction is near zero.
Simultaneous Weak Measurements
For simultaneous measurements we also did 20,000 simulations to obtain work and entropy probability distributions. For the simulations we use much weaker measurement strengths for x and z compared to single type measurements.
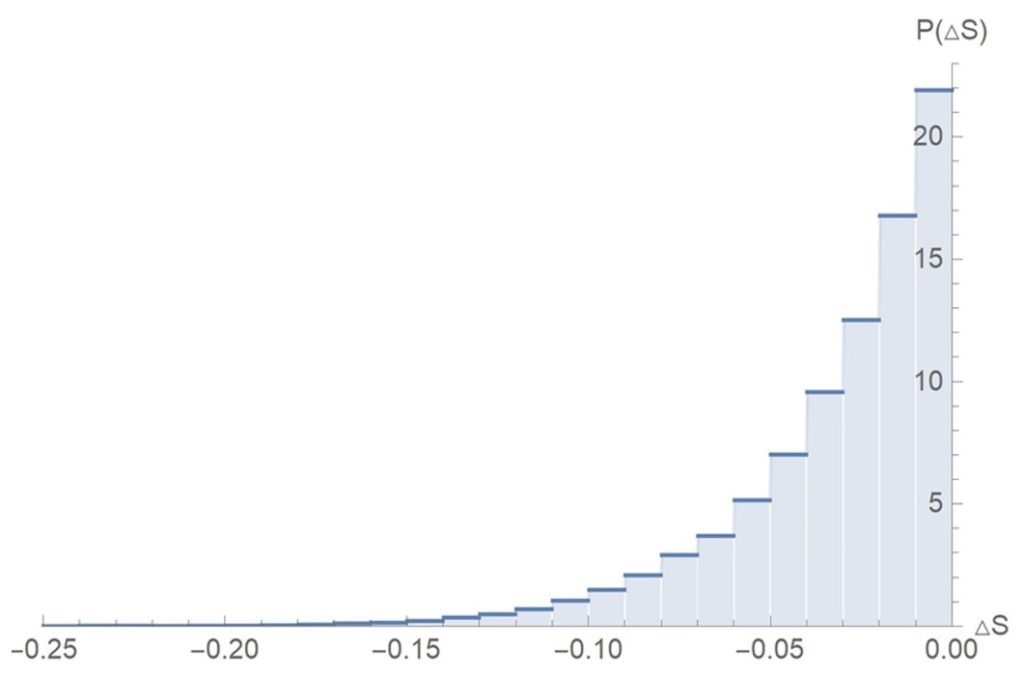
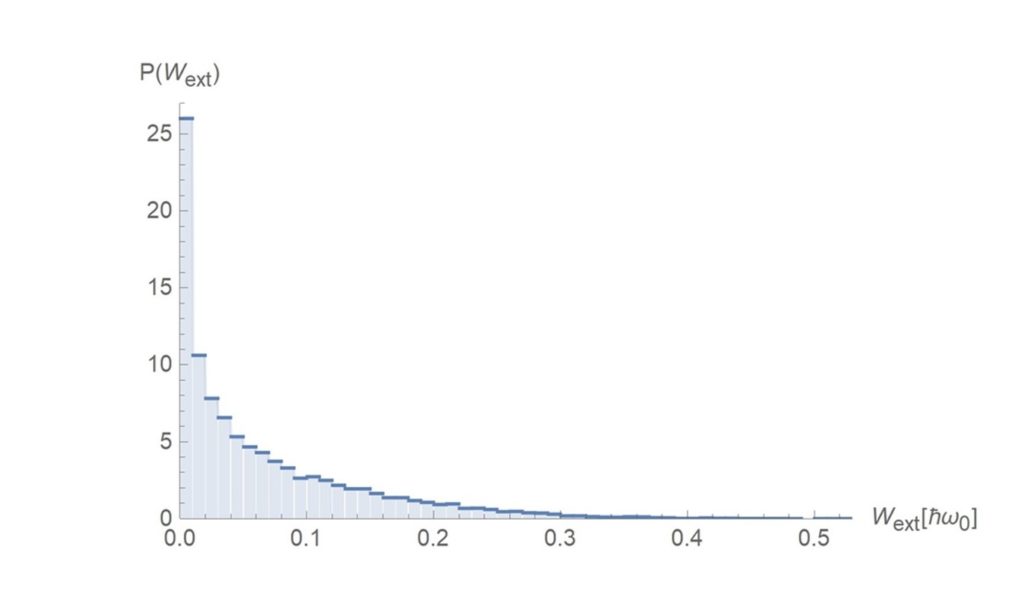
We obtain similar results as before, but now the probability distributions are more spread out. Work extraction has a much larger range than before.
